최근 크리스마스 전에 현관문을 장식하기 위해 별 모양이 필요했어요.
계획은 멋지게 폐박스에 그리고, 오려서 색칠 하는 것이었지요.
그래서 먼저 그려봤습니다.

하..
옆에서 보던 딸아이가 한숨을 쉬며,
"아빠 별이..좀 삐뚤 빠뚤 한데? "
하고 핀잔을 줍니다.
흠... 기다려 봐. 그럼 완벽한 별을 그려주마!!!
잠시 생각을 해보니 결국 별은 정 오각형을 그릴 수 있느냐? 의 문제였어요.
컴퍼스를 가져와서 종이에 이렇게 저렇게 해봤지만,
삼각형, 사각형, 육각형을 제외하고는 쉽사리 그려지지 않는다는 것을 알게 되었지요.
물론 그중에서도 5 각형은 "그냥 대충 한번 해보면 되겠지.. " 하는 마인드로는 안 되는 것이었어요.
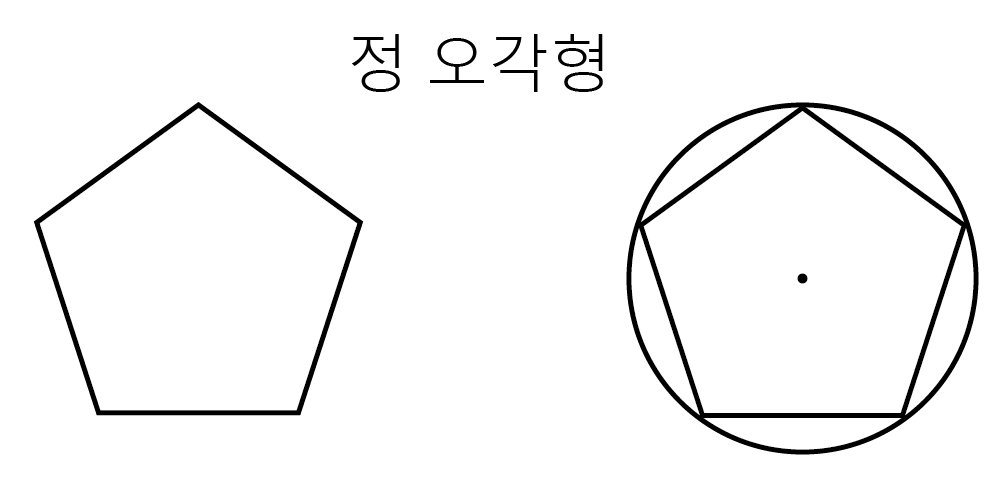
그래서 인터넷을 뒤져보니 컴퍼스를 이용해 정오각형을 그리는 작도법이 다양하게 나와 있더군요.
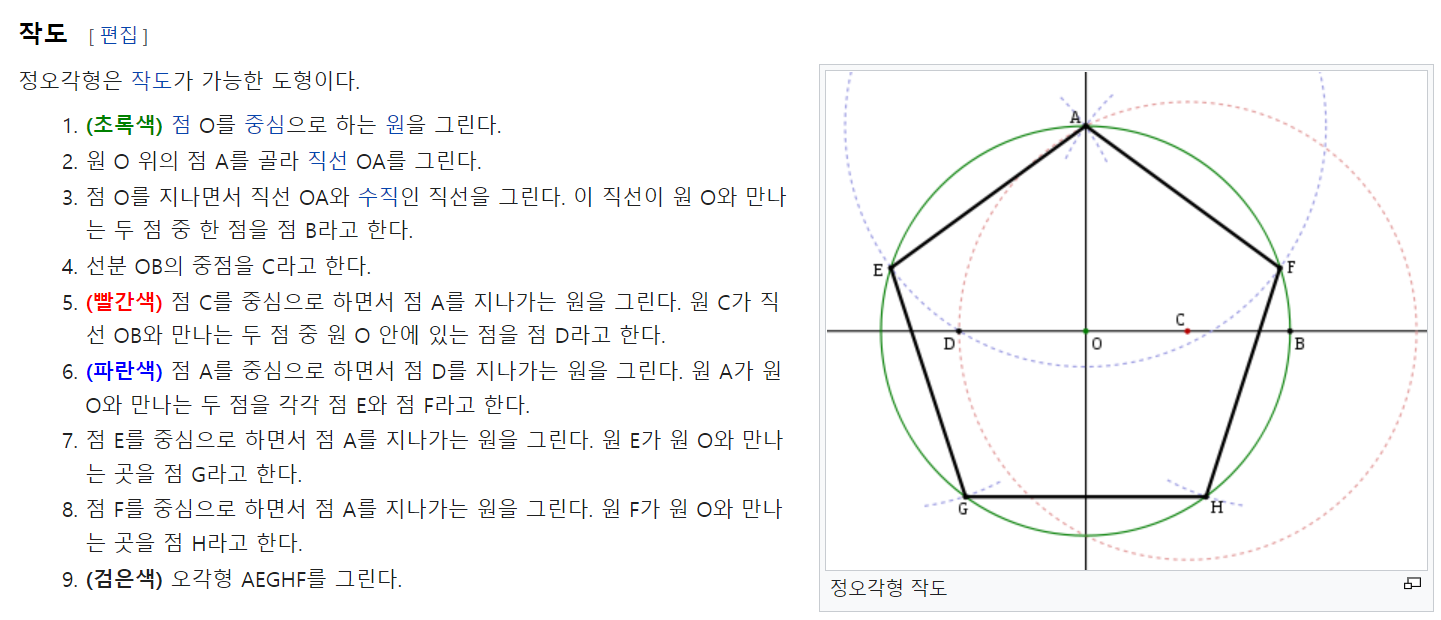
한번 따라 해 볼까.. 하고 시도를 해서 오각형을 그려보기도 했지만,
문득 "이거 내년에 또 그리려고 하면 기억이 안 나겠는데?? " 하는 생각이 들었어요.
그래서, 수치적으로 계산을 해 보면, 나중에 써먹기 좋겠다는 결론을 내렸지요.
그래서 오각형에 대해 잠시 고민을 해봤어요.
먼저 오각형은 원의 중심으로부터 모든 꼭짓점에 선을 연결했을 때 5개의 삼각형이 나오며,
중심부의 내각이 72 도임을 우리는 쉽게 알 수 있습니다.
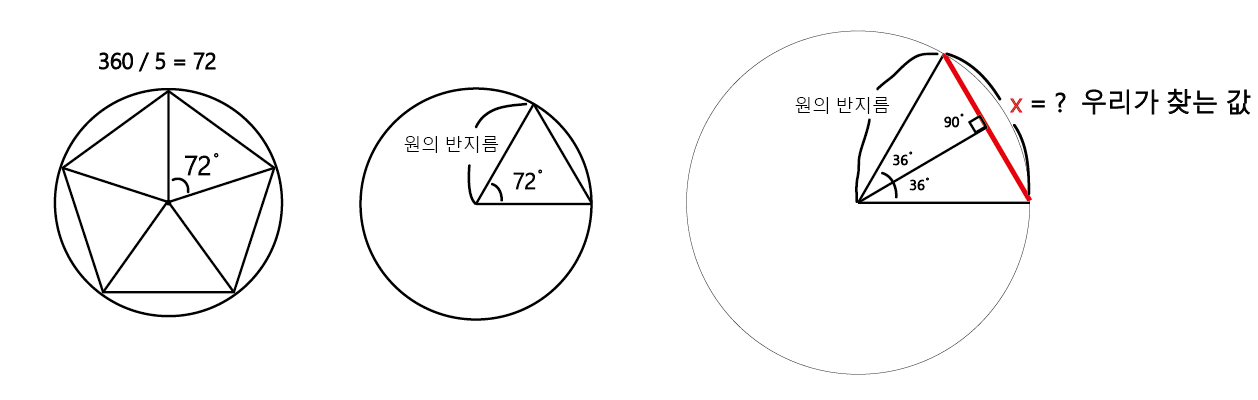
그렇다면, 원의 중심을 기준으로 그려진 이등변 삼각형의 밑변의 길이( X )만 알아내면 되는 것인 거죠.
그것이 바로 오각형의 한 변의 길이니까요. 후후훗.
( 계산을 용이하게 하기 위해 반지름을 5Cm로 하는 원을 기준으로 했어요. )
삼각비를 이용해서 쉽게 알아낼 수 있지요.
먼저 밑변을 반으로 나눠 직각 삼각형을 만들어줍니다.
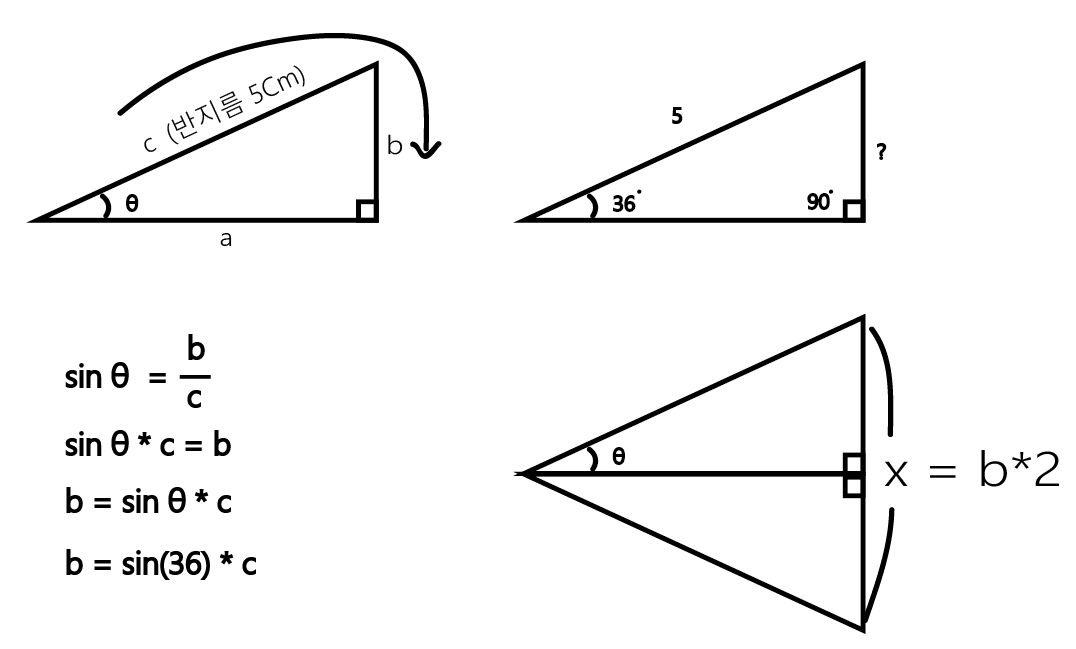
우리가 아는 것은 반지름과 기준각 세타입니다.
따라서 바로 그 sin 비율을 이용해 계산을 해보니 b는 sin(36) * c라는 것을 알게 되었지요.
자자 그럼 sin(36) 을 계산해 봅시다.
일단 sin(x) = a 의 일반 해를 구하는 공식은....
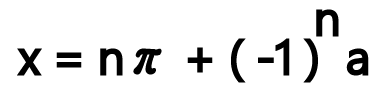
못 본 걸로 하시고,
계산기 때립니다.
일반 모드에서는 sin 값을 계산할 수 없으니 공학용으로 모드를 바꿔줍니다.
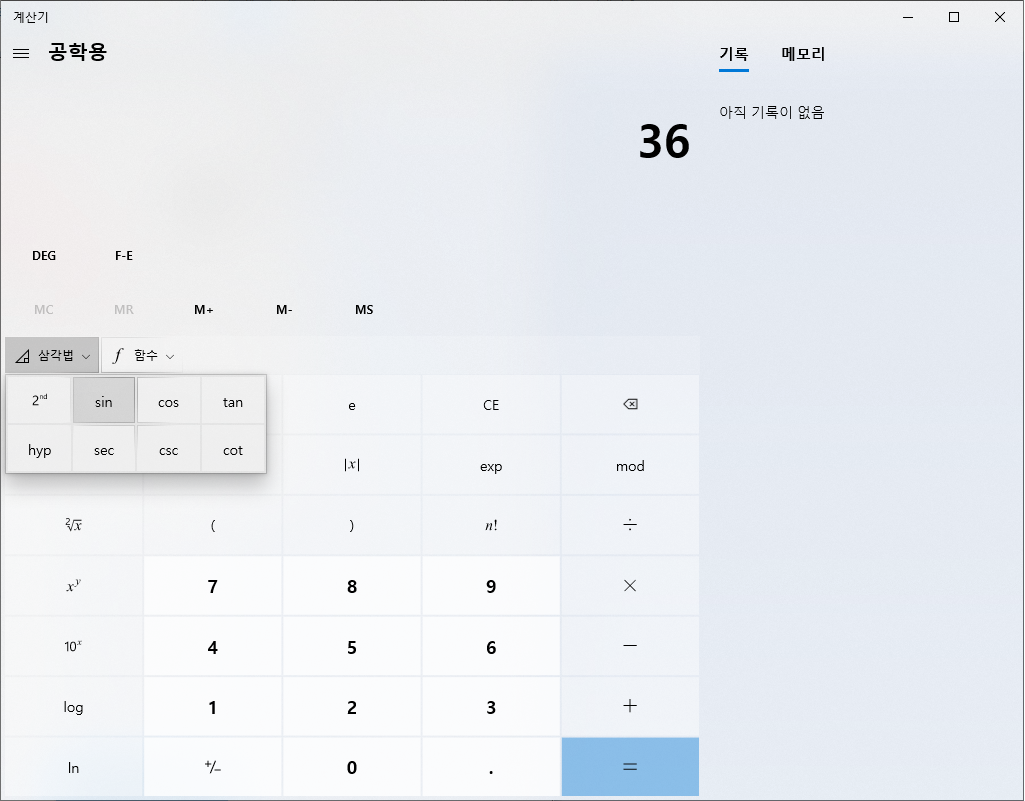

와우 간단하네요.
대략 0.5877852522924...어쩌고가 나왔군요
자, 이제 이 비율 값을 가지고 우리가 원하는 값 x 를 구해 봅시다
c = 반지름 = 5cm
sin(36) = 0.587785252...
b = 0.5877852522.. * 5 = 2.93892626..
x = b*2
x = 5.8778525229..
나왔습니다. !!
반지름이 5Cm 인 원은, 그 안에 그려지는 정 오각형의 한 변의 길이가 5.8778525229.. Cm라는 거지요.
준비는 다 됐습니다.
자, 이제 그려 봅니다.
먼저 반지름이 5Cm 인 원을 그려줍니다.
그리고, 폭이 5.8778525... Cm 가 되도록 컴퍼스를 최선을 다해 세팅합니다.
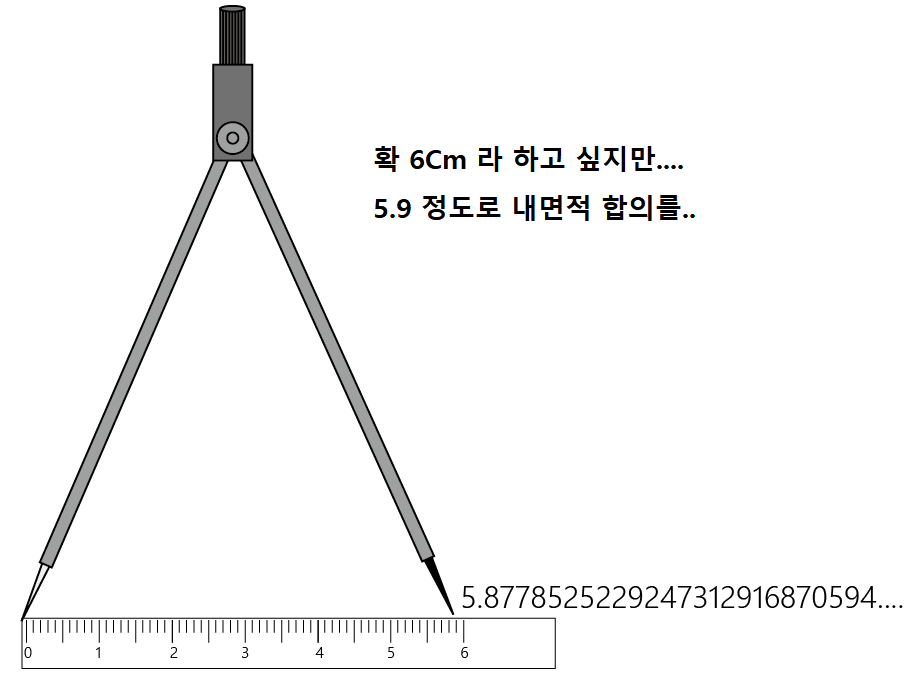
이제 그려진 원 위의 임의의 지점에 컴퍼스를 고정하고 원을 그려줍니다.
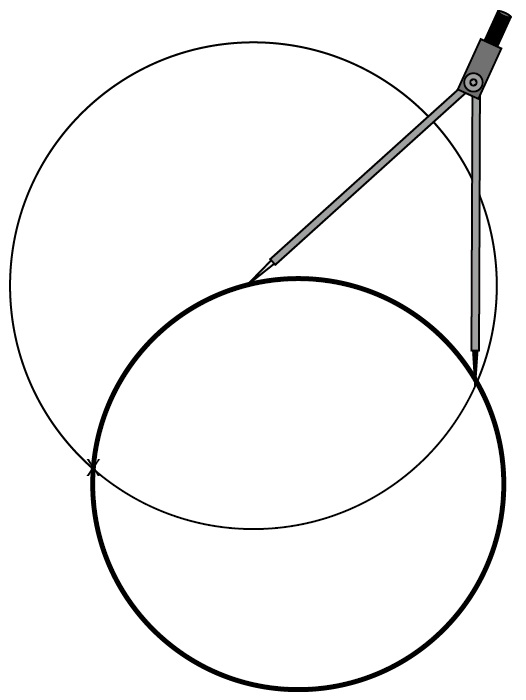
새로 그려진 원과 접합되는 부분을 기준으로 모든 원을 다 그려줍니다.
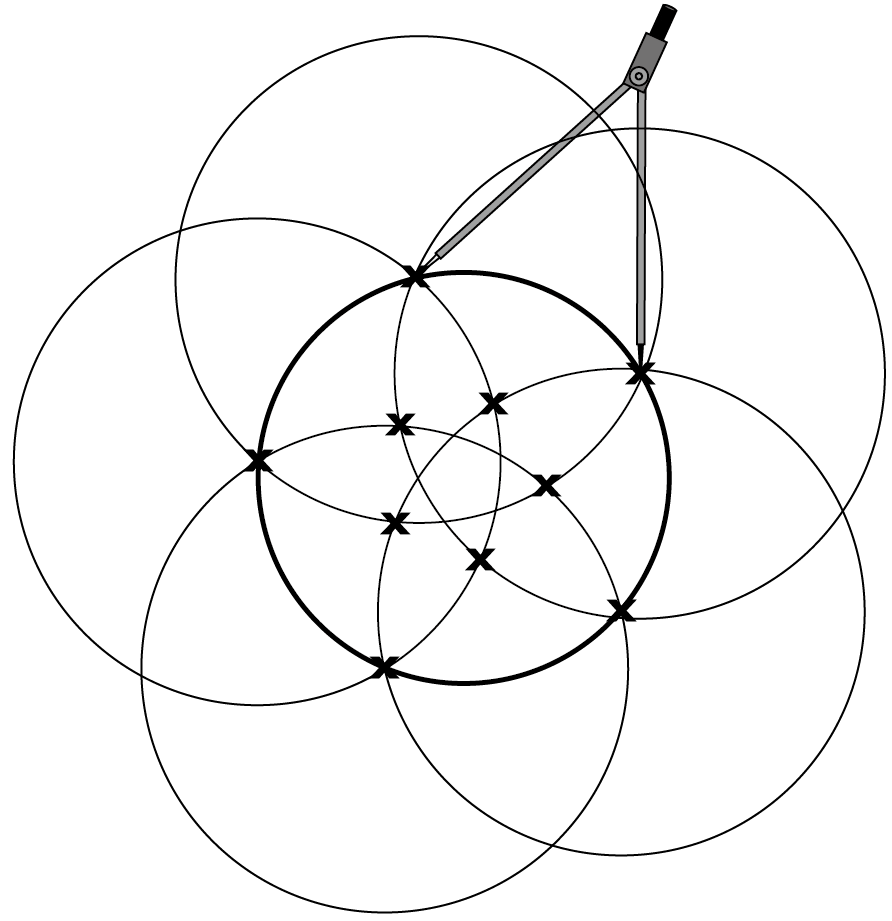
그럼 이렇게 멋진 모양이 나오지요.
이미 그 안에 별 모양이 보이는군요.
무려 두 개의 별과 오각정 오각형이 눈이 띕니다.
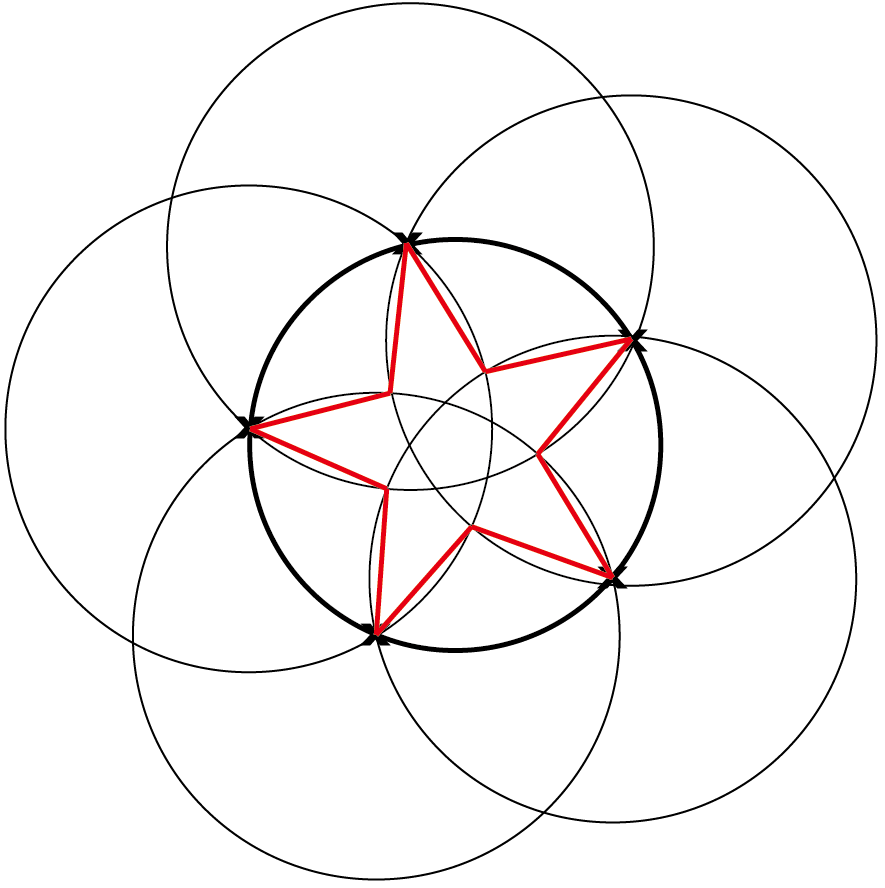
그려진 꼭짓점을 선으로 연결해 주면 됩니다.

이 거 시 바 로 완 벼 칸 비 열 !!!
정리를 하자면,
r ( 그린 원의 반지름 ) * 0.5877852522992473...*2 니까..
컴퍼스로 반지름을 특정한 원을 그려놓고,
원의 반지름(r) * 1.1755를 컴퍼스로 잡고 동그라미만 그려대면 된다는 겁니다.
좀 그럴싸하게 말하자면.
특정 원안에 그려지는 정 오각형 한 변의 길이(x) 를 구하는 공식은
x = sin(36) * r * 2
가 되겠습니다.
'아빠가 개발자면 생기는 일' 카테고리의 다른 글
| 배터리의 구조에 대한 기본적 이해와 충전 모듈 사용법. (3) | 2023.11.22 |
|---|---|
| 할로윈데이 !! (1) | 2022.11.01 |
| 할로윈데이 호박 유령 (잭 오 랜턴) 을 만들어봤어요 2 (0) | 2021.10.25 |
| 할로윈데이 호박 유령을 만들어봤어요 1 (0) | 2021.10.20 |
| 어린이 연습용 젓가락 개조 (0) | 2021.01.06 |





댓글